Bloque 3

CONTENIDOS DEL BLOQUE:

DISTRIBUCION DE PROBABILIDAD DE VARIABLES ALEATORIAS DISCRETAS

DISTRIBUCION BINOMIAL

DISTRIBUCION HIPERGEOMETRICA

ESPERANZA MATEMÁTICA O VALOR ESPERADO

TEOREMA DE BAYES DE PROBABILIDAD 

DISTRIBUCION DE PROBABILIDAD DE VARIABLES ALEATORIAS DISCRETAS

CONCEPTO:

Una variable discreta proporciona datos que son llamados datos cuantitativos discretos y son respuestas numéricas que resultan de un proceso de conteo.

 Ejemplos:

-La cantidad de alumnos regulares en un grupo escolar.

-El número de águilas en cinco lanzamientos de una moneda.

-Número de circuitos en una computadora.

 PROBLEMAS RESUELTOS:
Variable Aleatoria

Una variable aleatoria X puede tomar los valores 30,40,50 y 60 con probabilidades 0.4,0.2,0.1 y 0.3. Represente en una tabla la funci on de probabilidad, P(X=x), y la funci on de distribuci on de probabilidad, F (X) = P(X≤ x), y determine las siguientes probabilidades.

1.P(X≤25)

2.P(X≥60)

3.P(X <40)

4.P(X >40)

5.P(30≤X≤60)

6.P(30≤X <60)

7.P(30< X≤60)

8.P(30< X <60)

 

Obtenga la esperanza y varianza de X

 Ejemplo:

Distribuci on de probabilidad de X

 

Funci on de distribuci on de probabilidad de  X

 

 

C alculo de la Esperanza matem atica,E(X)

 

 Problema resuelto

Con la variable aleatoria X, cuya funci on de probabilidad viene dada en la tabla siguiente

 

1. Determine la esperanza y varianza

2. Determine la funci on de distribuci on de probabilidad

3. Determine F(33);F(14;5);F(3);P(10;5< X≤17;5)

 

 

 DISTRIBUCION BINOMIAL

Llamamos experiencia aleatoria dicotómica a aquella que sólo puede tener dos posibles resultados A y A'. Usualmente A recibe el nombre de éxito, además representaremos como p = p(A) y q = 1-p=p(A').
A la función de probabilidad de una variable aleatoria X resultado de contar el número de éxitos al repetir n veces una experiencia aleatoria dicotómica con probabilidad de éxito p la llamamos distribución binomial y la representamos por

B (n, p)

Para esta distribución se verifica que, la variable X puede tomar los valores:

0, 1, 2, ... , n

y que la variable toma cada uno de estos valores con probabilidad:

Problemas resueltos:
1) La última novela de un autor ha tenido un gran éxito, hasta el punto de que el 80% de los lectores ya la han leido. Un grupo de 4 amigos son aficionados a la lectura
 a) ¿Cuál es la probabilidad de que en el grupo hayan leido la novela 2 personas?

B(4, 0.2) p = 0.8 q = 0.2

b) ¿Y cómo máximo 2?

 2)Un agente de seguros vende pólizas a cinco personas de la misma edad y que disfrutan de buena salud. Según las tablas actuales, la probabilidad de que una persona en estas condiciones viva 30 años o más es 2/3. Hállese la probabilidad de que, transcurridos 30 años, vivan:
a)Las cinco personas

B(5, 2/3) p = 2/3 q = 1/3

b)Al menos tres personas

c)Exactamente dos personas

DISTRIBUCION HIPERGEOMÉTRICA
 A diferencia de la distribución Binomial, los elementos se extraen simultáneamente, o si es uno a uno, sin devolverlos antes de realizar la siguiente extracción, de forma que un elemento no puede aparecer dos veces en una muestra. A esta manera de obtener la muestra se le llama muestreo sin reemplazo.

 5 fabricantes producen en determinado dispositivo cuya calidad varia de un fabricante a otro. si usted elige 3 fabricantes al azar, hallar la probabilidad que la seleccion contenga 2 de las 3 mejores.
  

PROBLEMAS RESUELTOS

 

 

ESPERANZA MATEMÁTICA O VALOR ESPERADO
 La esperanza matemática o valor esperado de una variable aleatoria discreta es la suma del producto de la probabilidad de cada suceso por el valor de dicho suceso

 Los nombre de esperanza matemática y valor esperado tienen su origen en los juegos de azar y hacen referencia a la ganancia promedio esperada por un jugador cuando hace un gran número de apuestas.
 Si la esperanza matemática es cero, E(x) = 0, el juego es equitativo, es decir, no existe ventaja ni para el jugador ni para la banca.

PROBLEMAS RESUELTOS

Si una persona compra una papeleta en una rifa, en la que puede ganar de 5.000 € ó un segundo premio de 2000 € con probabilidades de: 0.001 y 0.003. ¿Cuál sería el precio justo a pagar por la papeleta?

E(x) = 5000 · 0.001 + 2000 · 0.003 = 11 €

Un jugador lanza dos monedas. Gana 1 ó 2 € si aparecen una o dos caras. Por otra parte pierde 5 € si no aparece cara. Determinar la esperanza matemática del juego y si éste es favorable.

E = {(c,c);(c,x);(x,c);(x,x)}

p(+1) = 2/4

p(+2) = 1/4

p(−5) = 1/4

E(x)= 1 · 2/4 + 2 · 1/4 - 5 · 1/4 = −1/4. Es desfavorable

TEOREMA DE BAYES DE PROBABILIDAD  

La interpretación más aceptada del teorema de Bayes, es que su estructura permite el calculo de probabilidades después de haber sido realizado un experimento (probabilidades aposteriori), basándose en el conocimiento de la ocurrencia de ciertos eventos que dependan del evento estudiado, o sea, se parte de probabilidades conocidas antes de efectuar el experimento (probabilidades apriori), las cuales son afectadas por las probabilidades propias del experimento (las que aparecen durante la ocurrencia del evento).

Continuando nuestro análisis sobre el teorema de Bayes, la probabilidad condicional de A_i dado B, para cualquier i, es:

Aplicando en el numerador la Regla de Multiplicación P(A_iÇB) = P(A_i) P(B|A_i) y en el denominador el Teorema de Probabilidad Total  P(B) = P(A₁) P(B | A₁) + P(A₂) P(B | A₂) + . . . + P(A_n) P(B | A_n), obtenemos la ecuación que representa al:

PROBLEMAS RESUELTOS
En la sala de pediatría de un hospital, el 60% de los pacientes son niñas. De los niños el 35% son menores de 24 meses. El 20% de las niñas tienen menos de 24 meses. Un pediatra que ingresa a la sala selecciona un infante al azar.
a. Determine el valor de la probabilidad de que sea menor de 24 meses.
b. Si el infante resulta ser menor de 24 meses. Determine la probabilidad que sea una niña.

SOLUCIÓN:

Se definen los sucesos:

Suceso H: seleccionar una niña.

Suceso V: seleccionar un niño.

Suceso M: infante menor de 24 meses.

En los ejercicios de probabilidad total y teorema de bayes, es importante identificar los sucesos que forman la población y cuál es la característica que tienen en común dichos sucesos. Estos serán los sucesos condicionados.

a. En este caso, la población es de los infantes. Y la característica en común es que sean menores de 24 meses. Por lo tanto, la probabilidad de seleccionar un infante menor de 24 meses es un ejemplo de probabilidad total. Su probabilidad será:

 

b. Para identificar cuando en un ejercicio se hace referencia al teorema de bayes, hay que partir de reconocer esta es una probabilidad condicionada y que la característica común de los sucesos condicionantes ya ha ocurrido. Entonces, la probabilidad de que sea niña una infante menor de 24 meses será:

Un médico cirujano se especializa en cirugías estéticas. Entre sus pacientes, el 20% se realizan correcciones faciales, un 35% implantes mamarios y el restante en otras cirugías correctivas. Se sabe además, que son de genero masculino el 25% de los que se realizan correcciones faciales, 15% implantes mamarios y 40% otras cirugías correctivas. Si se selecciona un paciente al azar, determine:
a. Determine la probabilidad de que sea de género masculino
b. Si resulta que es de género masculino, determine la probabilidad que se haya realizado una cirugía de implantes mamarios.

SOLUCIÓN:

Se definen los sucesos:

Suceso F: pacientes que se realizan cirugías faciales

Suceso M: pacientes que se realizan implantes mamarios

Suceso O: pacientes que se realizan otras cirugías correctivas

Suceso H: pacientes de género masculino

a. La probabilidad de que sea de género masculino se refiere a un problema de probabilidad total, ya que es el suceso condicionado y las cirugías los condicionantes. Dicho valor será:

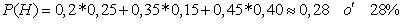
b. Como el suceso condicionado ha ocurrido entonces se aplica el teorema de bayes, luego, el valor de la probabilidad será: